信息学竞赛模板（八）— 数学相关

1. 素数筛

1.1 Eratosthenes筛（欧式筛）

• 时间复杂度 $O(n*loglogn)$

const int M = 1e6 + 5;
bool v[M];
vector<int> primes;

void calc_primes(){
    memset(v, true, sizeof(v));
    for(int i=2; i<=M; i++){
        if(v[i]){
            primes.push_back(i);
            for(int j=2; j<=M/i; j++) v[i*j] = false;
        }
    }
}

---

1.2 线性筛

• 时间复杂度 $O(n)$

const int N = 1e6 + 5;
int v[N], prime[N];
int m;

// n < N, 其中v[i] 记录了数字 i 的最小质因子
void primes(int n){
    memset(v, 0, sizeof v);
    m = 0;
    for(int i = 2; i <= n; i++){
        if(v[i] == 0){	//为质数
            v[i] = i;
            prime[++m] = i;
        }
        
        for(int j = 1; j <= m; j++){
            if(prime[j] > v[i] || prime[j] > n / i) break;
            v[i * prime[j]] = prime[j];
        }
    }
}

---

2. 质因数分解

2.1 定义

按照质因数分解定律，任何一个正整数（>=2）都可以被分解为如下形式：

$N = p_1^{c_1}*p_1^{c_2}*\cdots*p_m^{c_m}$

N的正约数个数 为：

$(c_1+1)*(c_2+1)*\cdots*(c_m+1)$

N的所有正约数的和 为：

$(1+p_1+p_1^2+...+p_1^{c_1})*\cdots*(1+p_m+p_m^2+...+p_m^{c_m})$

2.2 性质及推论

1. 一个整数 $N$ 的约数个数上界为 $2\sqrt{N}$ 。
2. $1\sim N$ 每个数的约数个数的总和大约为 $N\log_2^N$ 。
3. $1\sim N$ ($\le 2\times10^9$)中任何数的不同质因子都不会超过 $10$ 个，且所有质因子的指数总和不超过 $30$。

2.3 模板代码

pair<int, int> pc[10000];
int tot;

void divide(int n) {
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            int cnt = 0;
            while (n % i == 0) {
                cnt++;
                n /= i;
            }
            pc[tot++] = {i, cnt};
        }
    }
    if (n > 1) pc[tot++] = {n, 1};    //没分解完，必然为质数
}

改进，为了减少不必要的运算，用素数筛的结果 primes 数组代替 $i$ 进行“试除法“。（此处用了１中的素数筛后继续分解。）

//primes是素数筛的结果集合

pair<int, int> pc[10000];
int tot;

void divide(int n) {
    for (int i = 0; primes[i] * primes[i] <= n; i++) {
        auto p = primes[i];
        if (n % p == 0) {
            int cnt = 0;
            while (n % p == 0) {
                cnt++;
                n /= p;
            }
            pc[tot++] = {p, cnt};
        }
    }
    if (n > 1) pc[tot++] = {n, 1};    //没分解完，必然为质数
}

---

3. 约数

3.1 最大公约数

• 欧几里德算法

可使用 c++ 自带 __gcd(a, b) 函数

//不用考虑 a 和 b 的大小关系
int gcd(int a, int b){
    return b ? gcd(b, a % b) : a;
}

• 辗转相除法

int gcd(int a, int b) {
    if (a == b) return a;
    if (a < b) return gcd(b - a, a);
    return gcd(b, a - b);
}

3.2 最小公倍数

//不用考虑 a 和 b 的大小关系
int lcm(int a, int b){
    return a * b / gcd(a, b);
}

3.3 扩展欧几里德算法

存在整数 $x$ 和 $y$，使得 $ax + by = gcd(a, b)$ 成立。

int exgcd(int a, int b, int &x, int &y){
    if(b == 0){
        x = 1;
        y = 0;
        return a;
    }
    
    int d = exgcd(b, a % b, x, y);
    int z = x;
    x = y;
    y = z - y * (a / b);
    return d;
}

3.4 获取 n 的全部约数

$n <= 10^{14}$，复杂度 $O(\sqrt{n})$

vector<int> calc(LL n) {
    vector<int> nums;
    for (int i = 1; i <= n / i; i++) {
        if (n % i == 0) {
            nums.push_back(i);
            if (i * 1ll * i != n) nums.push_back(n / i);
        }
    }
    return nums;
}

---

4. 欧拉函数

4.1 定义

$1\sim N$ 中与 $N$ 互质的数的个数称为欧拉函数，表示为：

$\begin{aligned} \phi(N) &= N*\frac{p_1-1}{p_1}*\frac{p_2-1}{p_2}*...*\frac{p_m-1}{p_m} \\ &= N*\prod_{i=1}^m(1-\frac{1}{p_i}) \end{aligned}$

4.2 性质及推论

1. 任意$n>1$，$1\sim n$ 中与 $n$ 互质的数的和为 $n*\phi(n)/2$ 。
2. 若 $a,b$ 互质，则$\phi(ab) = \phi(a)\phi(b)$ 。
3. 当 $a,b$ 互质时，有 $f(ab)=f(a)f(b)$，那么称为函数 $f$ 为积性函数。
4. 若 $f$ 为积性函数，且在算数基本定理中 $n=\prod_{i=1}^mp_i^{c_i}$，则$f(n)=\prod_{i=1}^mf(p_i^{c_i})$ 。
5. 设 $p$ 为质数，若 $p|n$ 且 $p^2|n$，则 $\phi(n) = \phi(n/p)*p$ 。
6. 设 $p$ 为质数，若 $p|n$ 但 $p^2|n$，则 $\phi(n) = \phi(n/p)*p$ 。
7. $\sum_{d|n}\phi(d)=n$ 。

4.3 费马小定理

若 $p$ 为质数， 则对于任意整数 $a$，有 $a^p \equiv a \pmod p$ 。

4.4 欧拉定理

若正整数 $a, n$ 互质， 则有 $a^{\phi(n)} \equiv 1 \pmod n$，其中 $\phi(n)$ 为欧拉函数。

• 推论

  若正整数 $a, n$ 互质， 则对于任意正整数 $b$，有 $a^b \equiv a^{b\mod\phi(n)} \pmod n$ 。

4.5 模板代码

• 只计算 $n$ 的欧拉函数

//分解质因数的同时，即可顺便计算出欧拉函数
int phi(int n){
    int ans = n;
    for(int i = 2; i * i <= n; i++){
        if(n % i == 0){
            ans = ans / i * (i - 1);
            while(n % i == 0) n /= i;
        }
    }
    if(n > 1) ans = ans / n * (n - 1);
    return ans;
}

---

• 计算 $1 \sim n$ 中每个数的欧拉函数

const int N = 1e6 + 5;
int phi[N];

void euler(int n) {
    for (int i = 1; i <= n; ++i) phi[i] = i;
    for (int i = 2; i <= n; ++i) {
        if (phi[i] == i) {	//是质数，没有被处理过
            for (int j = i; j <= n; j += i) {
                phi[j] = phi[j] / i * (i - 1);
            }
        }
    }
}

• 改进，线性筛法

void pre() {
    phi[1] = 1;
    for (int i = 2; i <= N; ++i) {
        if (!v[i]) {
            phi[i] = i - 1;
            prime[++tot] = i;
        }
        for (int j = 1; j <= tot && i <= N / prime[j]; ++j) {
            v[i * prime[j]] = true;
            if (i % prime[j] == 0) {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
            phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
}

---

5. 莫比乌斯函数

5.1 定义

设正整数 $N$ 质因数分解后为 $N = p_1^{c_1}\times p_2^{c_2}\times \cdots \times p_m^{c_m}$，定义函数

$\mu(N) = \begin{cases} 1 & n = 1\\ 0 & n {\text{含有平方因子}}\\ (-1)^k & {\text{k 为 n 的本质不同因子个数}} \end{cases}$

---

称为莫比乌斯函数。

通俗的讲，当 $N$ 包含相同的质因子时， $\mu(N) = 0$。当 N 的所有质因子各不相同时，若因子个数为偶数个，则$\mu(N) = 1$，反之若为奇数个，则$\mu(N) = -1$。

5.2 性质及推论

1. $\sum_{d|n} \mu(d) = [n == 1] = \epsilon(n)$
2. 两积性函数 $f(n)$ 和 $g(n)$ 满足 狄利克雷卷积 ：$(f*g)(n) = \sum_{d|n}f(d)*g(\frac{n}{d})$
3. $\mu*1 = \epsilon$
4. 常用积性函数：
   • 单位函数：$\epsilon(n) = [n == 1]$
   • 恒等函数：$id_k(n) = n^k$，$id_1$常记为$id(n)$
   • 常数函数：$1(n) = 1$
   • 欧拉函数：$\phi(n) = \sum_{i = 1}^{n}[gcd(i,n) == 1]$（1~n 内与 n 互质的数的个数）
   • 莫比乌斯函数：同上 5.1 中的定义
5. 莫比乌斯反演：设 $f(n),g(n)$ 为两个数论函数。
   • 如果有 $f(n) = \sum_{d|n}g(d)$， 则有 $g(n) = \sum_{d|n}\mu(d)f(\frac{n}{d})$。
   • 如果有 $f(n) = \sum_{n|d}g(d)$， 则有 $g(n) = \sum_{n|d}\mu(\frac{d}{n})f(d)$。

5.3 模板代码

1. 求 $1\sim n$ 的每一项莫比乌斯函数

• 欧式筛

const int N = 1e6 + 5;
int miu[N];
bool v[N];

void calc(int n){
    for(int i = 1; i <= n; i++) miu[i] = 1, v[i] = false;
    for(int i = 2; i <= n; i++){
        if(v[i]) continue;
        miu[i] = -1;
        for(int j = 2 * i; j <= n; j += i){
            v[j] = true;
            if((j / i) % i == 0) miu[j] = 0;
            else miu[j] *= -1;
        }
    }
}

• 线性筛

const int N = 1e6 + 5;
int miu[N];
bool v[N];

void pre(int n) {
    miu[1] = 1;
    for (int i = 2; i <= n; ++i) {
        if (!v[i]) miu[i] = -1, p[++tot] = i;
        for (int j = 1; j <= tot && i <= n / p[j]; ++j) {
            v[i * p[j]] = 1;
            if (i % p[j] == 0) {
                miu[i * p[j]] = 0;
                break;
            }
            miu[i * p[j]] = -miu[i];
        }
    }
}

---

6. 乘法逆元

6.1 定义

要求 $a/b \mod n$ ，因为除法不满足 $a/b \mod n = (a \mod n)/(b \mod n)$。

因此，需要其他办法来解决此问题。

乘法逆元 即为用来解决此问题的数。

• 定义：

若整数 $b, m$ 互质，并且 $b | a$， 则存在一个整数 $x$， 使得 $a/b \equiv a*x \pmod m$。则称 $x$ 为 $b$ 的模 $m$ 乘法逆元，记为 $b^{-1}\pmod m$。

由 费马小定理 可知：对于两正整数 $a, n,n$ 为质数，且 $a < n$， 有

$a^n \equiv a \pmod n$

则可以等价于

$a^{n-1} \equiv 1 \pmod n$

则当模数为 $n$ 时， $a$ 的乘法逆元可以表示为 $a^{n - 2}$。

6.2 模板代码

• 扩展欧几里得算法

要求 $a$ 和 $b$ 互质，即 $gcd(a, b) = 1$，$x$ 为 $a$ 模 $b$ 的逆元，$y$ 为 $b$ 模 $a$ 的逆元。

void exgcd(int a, int b, int& x, int& y) {
    if (b == 0) {
        x = 1, y = 0;
        return;
    }
    exgcd(b, a % b, y, x);
    y -= a / b * x;
}

• 快速幂

要求 $n$ 为质数即可，$a$ 模 $p$ 的逆元为 $a^{p-2}$（费马小定理可知）。

int quick_pow(long long a, int n, int p) {
    int ans = 1;
    a = (a % p + p) % p;
    while(n){
        if (n & 1) ans = (a * ans) % p;
        a = (a * a) % p;
        n >>= 1;
    }
    return ans;
}

---

7. 差分矩阵

//以左上角(x1,y1)和右下角(x2, y2)确定的矩阵每个位置+c，其差分矩阵变化
void insert(int x1, int y1, int x2, int y2, int c){
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

//将差分矩阵复原为原矩阵
for(int i = 1; i <= m; i++){
    for(int j = 1; j <= n; j++){
	b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];    
    }
}

8. 数论分块

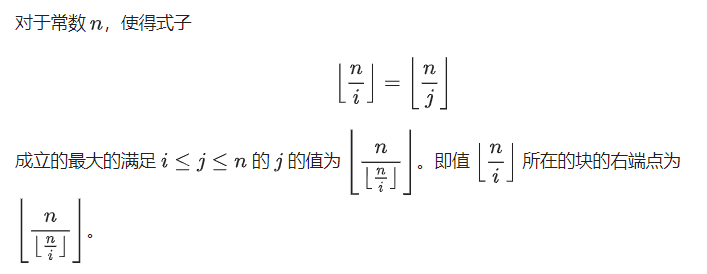
例题

题意： 给定一个整数 $n$，输出 $\sum_{i=1}^{n}\frac{n}{i}$ 。

思路：如上推导，对于每一块相同的 $\lfloor \frac{n}{i} \rfloor$ 一起计算。时间复杂度为 $O(\sqrt{n})$。

//核心代码
long long H(int n) {
    long long res = 0;  // 储存结果
    int l = 1, r;       // 块左端点与右端点
    while (l <= n) {
        r = n / (n / l);  // 计算当前块的右端点
        res += (r - l + 1) * 1LL * (n / l);  // 累加这一块的贡献到结果中。乘上 1LL 防止溢出
        l = r + 1;  // 左端点移到下一块
    }
    return res;
}